基本情報技術者試験の令和7年度の公開問題(科目A)を解こう。
今回のテーマは、「アローダイアグラム」である。
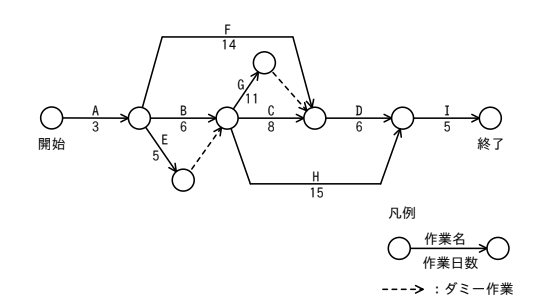
問14 図は,あるプロジェクトの作業 A ~ I とその作業日数を表している。このプロジェクトの最短所要日数は何日か。
ア 27
イ 28
ウ 29
エ 31
正解:エ
この問題は、プロジェクト管理でよく使われる「アローダイアグラム(PERT図)」の読み取りに関するものである。
「最短所要日数」を求める問題だが、これは言い換えると、「すべての作業が終わるまでに、どうしてもかかってしまう一番長い道のり(クリティカルパス)」を探す作業になる。
計算のコツは、「各地点にたどり着くまでの最大の日数」を順番にメモしていくことである。
解き方のステップ
1. 各結合点(○)の「最短開始日」を書き出す
図の左から順に、それぞれの○の地点に何日目に到達できるか計算する。道が合流するところでは、日数が大きい方(遅い方)を採用する。なぜなら、前の作業がすべて終わらないと次へ進めないからです。
- 作業Aのあと: 0 + 3 = 3日
- 作業BとEの合流地点:
- 上ルート(B):3 + 6 = 9日
- 下ルート(E+ダミー):3 + 5 + 0 = 8日
- 大きい方の 9日 を採用する。
- 作業C・G(ダミー経由)の合流地点:
- 上ルート(C):9 + 8 = 17日
- 下ルート(G+ダミー):9 + 11 + 0 = 20 日
- 大きい方の20日 を採用する。
- 作業Dの合流地点:
- 上ルート(D):20 + 6 = 26日
- 下ルート(H):9 + 15 = 24 日
- 大きい方の 26日 を採用する。
- 最後の作業Iのあと:
- 26 + 5 = 31日
このプロジェクトで最も時間がかかる経路(クリティカルパス)は、A → B → G → (ダミー) → D → I のルートになり、合計日数は 31日 である。
したがって、正解は エ となる。
まとめ
- ダミー作業(点線): 日数は「0」として計算する。
- 合流地点: 複数の矢印が集まる場所では、「一番大きい数字」を選ぶ(すべての準備が整うのを待つ必要があるため)。
- 最短所要日数: 言葉は「最短」だが、実際には「最も長い経路の合計」を指す。




コメント