基本情報技術者試験の令和7年度の公開問題(科目B)を解こう。
今回のテーマは、「同じ値を返す2つの関数」である。
令和7年度 基本情報技術者試験 科目 B 公開問題 問1
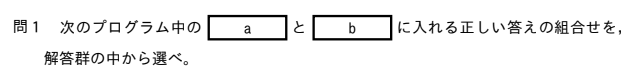


令和7年度 基本情報技術者試験 科目 B 公開問題
正解:カ
「効率的なカウント」の仕組みを見抜こう
この問題は、「愚直なやり方(function1)」と「賢いやり方(function2)」を比較する、アルゴリズムの基礎が詰まった良問である。
1. そもそも何をしたいプログラム?
このプログラムの目的は、「$n$ から $m$ までの間に、4の倍数がいくつあるか数える」ことである。
- function1(愚直): $n$ から $m$ まで1つずつチェックして、「4で割り切れる?」と聞いて回るスタイル。確実だが、範囲が広いと時間がかかる。
- function2(賢い): 最初の4の倍数を見つけたら、あとは4飛び(4, 8, 12…)で一気に数えるスタイル。計算量が少なくて済む。
2. 空欄 a の考え方:最初の「4の倍数」を見つけ出せ!
function2 の最初の for 文(空欄 a)の役割は、「$n$ 以上の数で、最も小さい4の倍数(tempN)を探し出すこと」である。
tempN ← n
for ( a )
if ((tempN mod 4) が 0 と等しい)
繰返し処理を終了する
endif
tempN ← tempN + 1
endforここで「何回繰り返せば、確実に4の倍数にぶつかるか?」を考える。
4の倍数は4つに1つの間隔で現れる。
- $n$ が 4の倍数なら:0回で見つかる。(例)8
- $n$ が「4の倍数+1」なら:3つ進めば見つかる。(例)9→12
- $n$ が「4の倍数+2」なら:2つ進めば見つかる。(例)10→12
- $n$ が「4の倍数+3」なら:1つ進めば見つかる。(例)11→12
まとめると
- あまり3(11など):1回でOK
- あまり2(10など):2回でOK
- あまり1(9など):3回必要!
一番遠いパターンに合わせて 「1から3まで」 ループを回す必要がある、ということになる。
つまり、最大でも3回チェックして、最大3回 tempN をインクリメントすれば、必ず4の倍数に到達する。
したがって、空欄 a は 「i を 1 から 3 まで 1 ずつ増やす」 が正解となる。
(※1から2までだと、運が悪いと4の倍数に届かない可能性がある。)
3. 空欄 b の考え方:4飛びで一気にカウント!
さて、tempN が無事に「最初の4の倍数」になった。ここからは、ゴールである $m$ まで一気にカウントする。
for ( b )
count ← count + 1
endforすでに tempN は4の倍数だと分かっているので、1つずつ調べる必要はない。4ずつ増やしていけば、その数はすべて4の倍数である。
- 開始地点:
tempN - 終了地点:
mを超えない範囲 - 増分:4ずつ
これに合致する選択肢を探すと、「j を tempN から始めて m を超えない範囲で 4 ずつ増やす」 となる。
ここまでの考察をまとめると、
- a:i を 1 から 3 まで 1 ずつ増やす
- b:j を tempN から始めて m を超えない範囲で 4 ずつ増やす
これを解答群から選ぶと、正解は 「カ」 になる。
5. 攻略のアドバイス
この問題のポイントは、「具体例で考えること」である。
例えば「$n=5, m=15$」と置いてみよう。
tempNは 5。aのループで、5(ダメ)→6(ダメ)→7(ダメ)と進み、ループ終了後にtempNは 8 になる。bのループで、8から始めて「8, 12」と4ずつ増え、結果は2個になる。function1で 5〜15 の4の倍数を探すと「8, 12」で、同じ2個になる。
アルゴリズム問題で迷ったら、小さな数字を当てはめてみるのが合格への近道!




コメント